|
Getting your Trinity Audio player ready...
|
Normality Test
A normality test determines whether a sample data has been drawn from a normally distributed population. It is generally performed to verify whether the data involved in the research have a normal distribution. Many statistical procedures such as correlation, regression, t-tests, and ANOVA, namely parametric tests, are based on the normal distribution of data.
What is Normal Distribution?
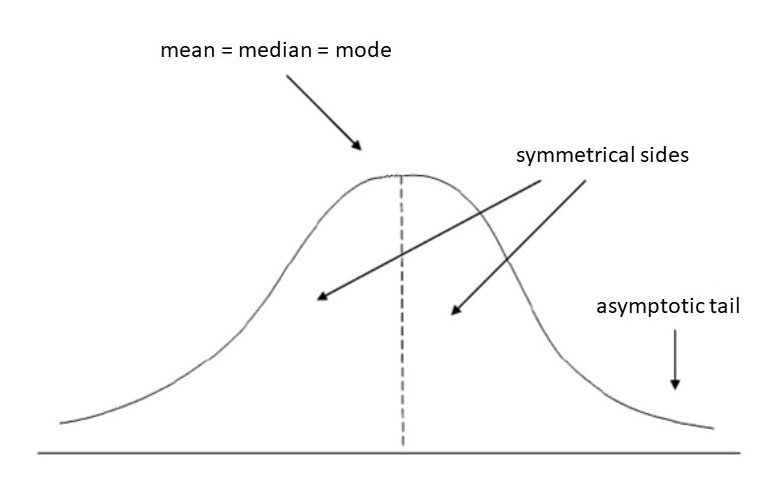
Normal distribution, also known as Gaussian distribution, is the most important statistical probability distribution for independent random variables. Most researchers will recognize it as the familiar bell-shaped curve present in statistical reports. Normal distributions are appropriate for continuous variables. It is a probability distribution that is symmetric about the mean, i.e., the right side is a mirror image of the left side, indicating that the data near the mean occur more frequently than those at a distance from the mean. The area under the normal distribution curve represents the probability, and the total area under the curve sums up to one. In a perfectly normal distribution, the mean, median, and mode values are the same, and they indicate the peak of the curve.
Methods of Assessing Normality
There are several methods to assess whether data are normally distributed, and they fall under two broad categories Graphical—such as histogram, Q-Q probability plot—and Analytical—such as Shapiro–Wilk test, Kolmogorov–Smirnov test.
Graphical Method of Assessing Normality
The most useful method of visualizing the normality distribution (or lack thereof) of a certain variable is to plot the data on a graph called as a frequency distribution chart or histogram.
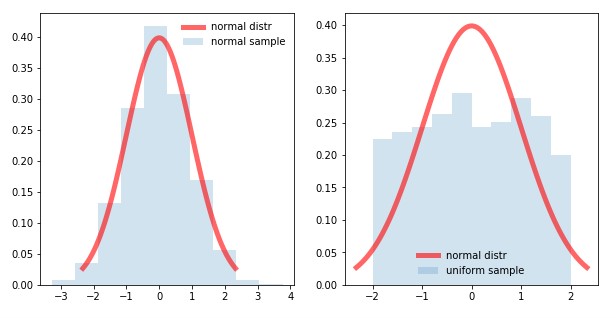
The normal distribution in Figure 2 shows a slight deviation of the actual sample distribution (gray bars) from the theoretical normal distribution curve (red line). This indicates that the given data are normally distributed. In the non-normal distribution in Figure 2, the sample deviated from the normal distribution. Graphical methods are typically not very useful when the sample size is small.
Analytical Method of Assessing Normality
We begin with the most basic data-analysis process. When analyzing the data, aggregate (collated) information is obtained from many data points, so it is important to present such aggregate data truthfully, i.e., in a way that best represents the dataset. Normally distributed data are best, and most truthfully, represented through mean and standard deviation. The arithmetic mean is the value obtained through the summation of all the values and dividing that by the number of observations, and the standard deviation is the measure of the dispersion of the variable (low standard deviation indicates low dispersion, i.e., grouping around the mean; a high standard deviation indicates high dispersion, i.e., values frequently tend to lie at the tails or are distant from the center or mean). In contrast, non-normally distributed values tend not to be well represented using these values but tend to be better reflected in the median and interquartile range.
The first step that we must undertake to check if the distribution of the variable follows the normal distribution is to conduct normality testing, which can usually be performed using some of the standard tests that are part of most statistical programs and applications, such as the
Kolmogorov–Smirnov, Shapiro–Wilk, and D’Agostino–Pearson tests. These tests analyze the data to verify if their distribution deviates significantly from the normal distribution using several parameters, such as the well-known p-value. If the p-value is <0.05, the distribution deviates significantly from the normal distribution.
Parametric tests are used when the distribution closely follows the normal distribution; otherwise, non-parametric tests are employed.
For two groups of data, the most widely used parametric test is the t-test (for independent or paired samples, depending on our data), and the non-parametric equivalent is the Mann–Whitney test. For more than two groups of data, the parametric test used is ANOVA, and its non-parametric equivalent is the Kruskal–Wallis test.
For correlations, the parametric test used is the Pearson correlation test, and its non‑parametric equivalent is the Spearman rank-correlation test.
It is important to note that using the wrong test (e.g., parametric for non-normally distributed data or non-parametric for normally distributed data) can result in completely wrong findings. This may falsely represent statistically significant findings as non-significant or non-significant findings as statistically significant!
Similarly, when conducting a regression analysis, it is important to bear in mind that the normal distribution of data is an important assumption for correctly performing most types of regression analysis. In other words, it is not possible to perform most forms of regression with non‑normally distributed variables. These variables may have to be transformed in some way (e.g., log-transformation, root-transformation, etc.) to ensure a normally distributed transformed variable. This is often overlooked when conducting statistical analyses and may lead to erroneous findings.
We hope this brief review explained the importance of normality of the distribution of variables and provided you with information on presentation and visualization of data according to normality, normality testing, and the potential pitfalls of not performing the tests properly. We plan to provide the next steps of statistical analysis in our upcoming blog posts.
If you want to know more about our Statistical Analysis and Review Service, click here.


Comment